点到平面的距离是立体几何中常见问题之一，根据不同条件选择不同方法，快速解决问题。本期将为大家介绍高考数学中，点到平面的距离公式是什么？怎么求？等问题一一解答。同时大家还可以关注高考100网站，进入网站查询更多内容。

一、点到平面的距离公式

点到平面距离是指空间内一点到平面内一点的最小长度。

点到平面的距离公式为：

1、d=|Ax0+By0+Cz0+D|/√(A²+B²+C²)

公式中的平面方程为Ax+By+Cz+D=0，点P的坐标(x0，y0，z0)，d为点P到平面的距离。

2、d=向量AB×向量n的和的模长÷向量n的模长

d表示点A到面的距离，向量AB是以点A为起点，以平面上任意一点为终点的向量，向量n是平面的法向量。点到平面距离是指空间内一点到平面内一点的最小长度。特殊的，当点在平面内时，该点到平面的距离为0。

二、点到平面的距离怎么求？

点到平面的距离通常包括：

1、直接法：作出垂线段，解三角形。

2、等积法：利用三棱锥体积公式求解。

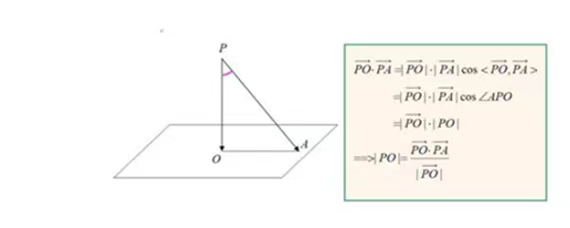
3、向量法：利用公式d=向量AB×向量n的和的模长÷向量n的模长。

三、更多内容

此外，还可以查看圆梦志愿通过大数据分析和云计算，为大家科学评估出的分数对应的所有可以就读的大学。