高中数学柯西不等式公式是什么？本期为大家整理柯西不等式的一般形式和推导过程，同时附上柯西不等式6个基本公式，供大家做高考数学大题时参考。

更多知识点、分数线、高考资讯等，我们可以从本文下方的“输入分数看能上的大学”一栏，输入自己的成绩、所在省、选考科目，一键进入圆梦志愿直接查看！

同时还可以查看圆梦志愿通过大数据分析及云计算处理，为我们科学评估出的分数对应的所有可以报考的院校。

一、高中柯西不等式公式

有关柯西不等式的内容在高考大纲中是“了解”，但是了解并不意味不考，在2019年全国3不等式选讲题目中就出现了柯西不等式的题目，此外柯西不等式还是江苏选做题中常见题型，虽然每年都不难。

柯西不等式的二维形式相比于均值不等式来说更加简单，因为它没有类似于均值不等式拼凑所具有的技巧性，在目前考柯西不等式的试卷中，即便出现也很容易解出，此外，柯西不等式还是解决三元不等式最值的好帮手，在高一数学中有一类值域问题，即函数由两个根式相加的形式组成，且满足x的系数互为相反数，这种题目可用三角换原来解，但是用柯西不等式更为简单，希望有关内容能引起学生重视。

柯西不等式和均值不等式比较，它并不要求变量始终满足正数；和均值不等式类似，利用柯西不等式求最值依旧要满足特定的等式要求，使用柯西不等式时满足“定”“等”即可。

下图为柯西不等式：

区别于均值不等式，可以把柯西不等式记作：和有最大值，积有最小值，求最大值时需要补项，使得右侧为定值即可。

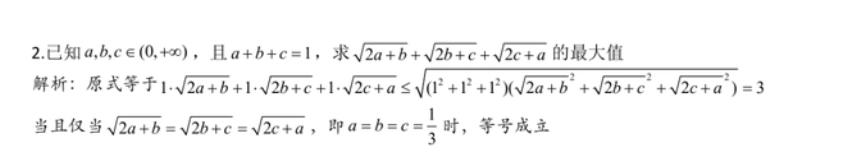
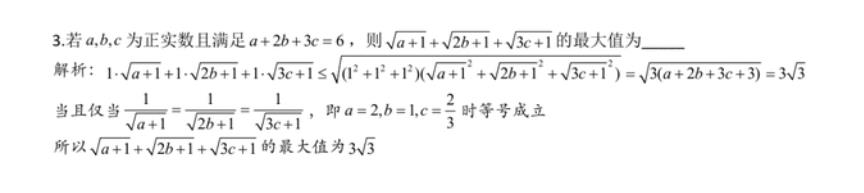
以上四题为利用柯西不等式求最大值，至于式子前补多少系数需要根据条件中的等式决定，如不确定系数可利用待定系数法设出系数，根据右侧的定值来确定系数的值。

二、柯西不等式的形式

1. 一般形式

2. 二维形式

3. 向量形式、三角形式、概率论形式、积分形式

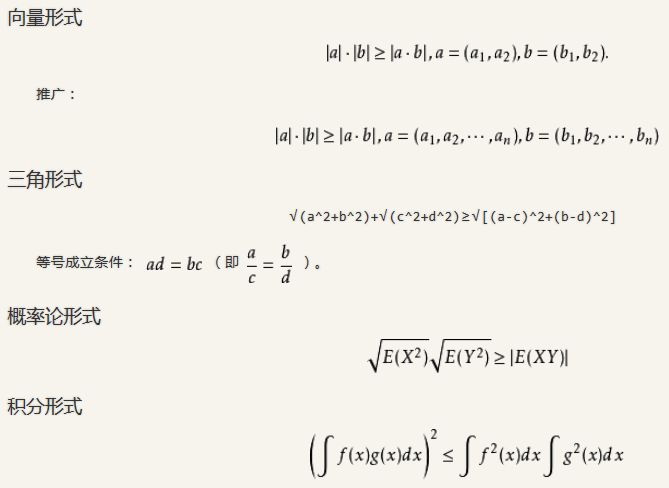
三、更多内容

大家从本文下方“输入分数看能上的大学”一栏，输入成绩、地区、选考科目，一键进入圆梦志愿，查看更多大学投档线线、专业分数线及位次、大学排名等数据。

同时圆梦志愿还可以通过大数据分析及云计算处理，为我们科学评估所有能上的大学以及被录取的概率，方便我们后续志愿填报选择学校参考！