今天来说说怎么样确定函数的单调性。

1用定义证明函数的单调性，可以用作差法，也可以用作商法。

无论是作差还是作商，步骤都是一样的，一共是四步。

第一步：取值，在题干指定的区间内，取x1 ，x2 ，令x1小于 x2。

第二步：变形，作差或者作商，并把式子进行变形，变形的方法有因式分解、配方、通分、分母有理化。变形的方向是作差法方便与0比较，作商法方便与1比较。

第三步：定号，确定作差或者作商的结果。如果不能确定，考虑分类讨论。

第四步：定论，根据x1与x2 的大小关系，f(x1)与 f(x2)的大小关系，结合单调性定义得出结论。

举个例子，

2图像法

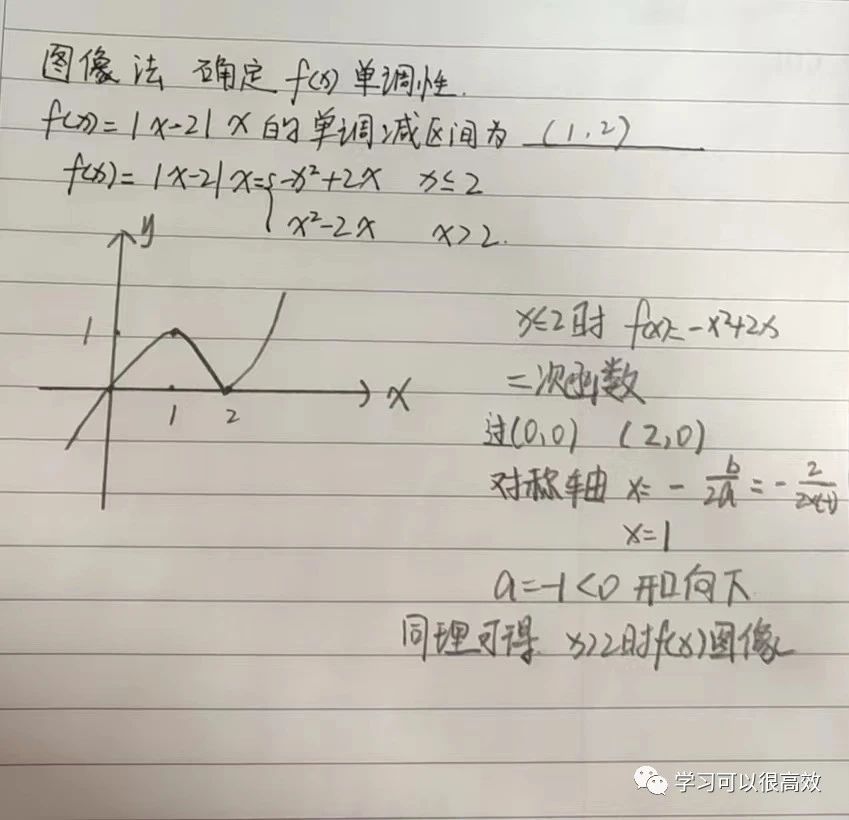
图像法确定函数的单调性，一定要先化简函数解析式，再画出它的草图，最后根据函数的定义域并结合草图，确定函数的单调区间。

当函数的解析式中含有绝对值时，要利用绝对值内等于0的分界点讨论，去掉绝对值符号，将函数转化为分段函数。

要想能画出图，学生一定要掌握二次函数，幂函数，指数函数，对数函数，三角函数的基本性质。比如二次函数的开口，对称轴。

3根据对称性

函数y=f(x)的图像关于直线x=a对称等同于f(x+a)=f(a-x)等同于f(x)=f(2a-x)。到对称轴距离相等的自变量对应的函数值相等。

函数y=f(x)与函数y=f(-x)的图像关于y轴对称。

4根据奇偶性 -"奇同偶异"

奇函数在关于原点对称的区间上有相同的单调性，偶函数在关于原点对称的区间上有相反的单调性，可以简记为"奇同偶异"。

5复合函数的单调性 -“同增异减”

判断复合函数y=f(g(x))的单调性的步骤，

第一步：定义域优先，拆分前必须确定函数的定义域。

第二步：将复合函数分解成y=f(u)与u=g(x)。

第三步：分别确定这两个函数的单调性。

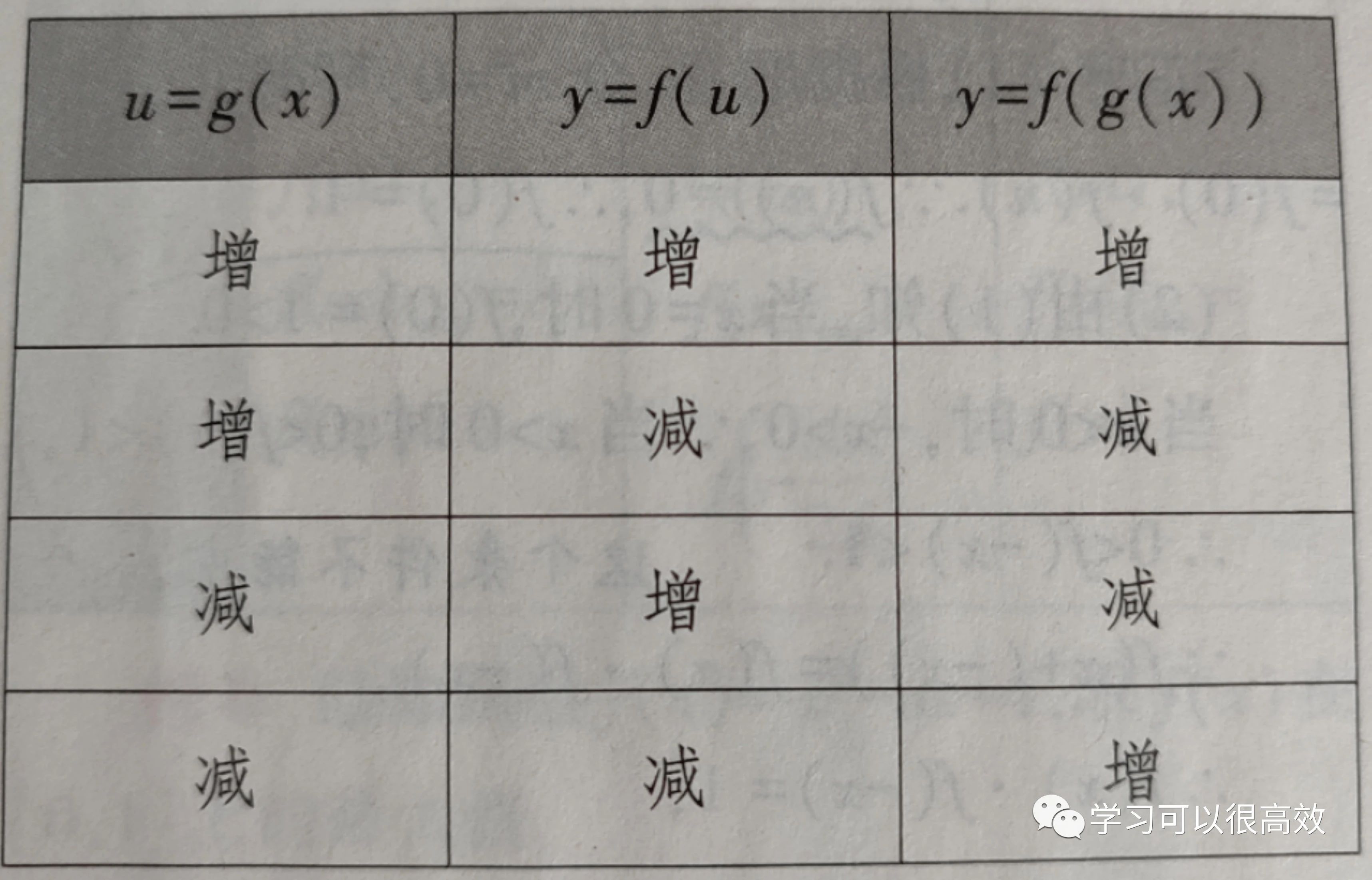
第四步：用"同增异减"判断函数 y=f(g(x))的单调性。

“同增异减”的意思如下图：

举个例题，